By Jason Smith

The inspiration for this piece came from a Vox podcast with Chris Hayes of MSNBC. One of the topics they discussed was which right-of-center ideas the left ought to engage. Hayes says:

The entirety of the corpus of [Friedrich] Hayek, [Milton] Friedman, and neoclassical economics. I think it’s an incredibly powerful intellectual tradition and a really important one to understand, these basic frameworks of neoclassical economics, the sort of ideas about market clearing prices, about the functioning of supply and demand, about thinking in marginal terms.

I think the tradition of economic thinking has been really influential. I think it’s actually a thing that people on the left really should do — take the time to understand all of that. There is a tremendous amount of incredible insight into some of the things we’re talking about, like non-zero-sum settings, and the way in which human exchange can be generative in this sort of amazing way. Understanding how capitalism works has been really, really important for me, and has been something that I feel like I’m a better thinker and an analyst because of the time and reading I put into a lot of conservative authors on that topic.

Putting aside the fact that the left has fully understood and engaged with these ideas, deeply and over decades (it may be dense writing, but it’s not exactly quantum field theory), I can hear some of you asking: Do I have to?

The answer is: No.

Why? Because you can get the same understanding while also understanding where these ideas fall apart ‒ that is to say understanding the limited scope of market-clearing prices and supply and demand – using information theory.

Prices and Hayek

Friedrich Hayek did have some insight into prices having something to do with information, but he got the details wrong and vastly understated the complexity of the system. He saw market prices aggregating information from events: a blueberry crop failure, a population boom, or speculation on crop yields. Price changes purportedly communicated knowledge about the state of the world.

However, Hayek was writing in a time before information theory. (Hayek’s The Use of Knowledge in Society was written in 1945, a just few years before Claude Shannon’s A Mathematical Theory of Communication in 1948.) Hayek thought a large amount of knowledge about biological or ecological systems, population, and social systems could be communicated by a single number: a price. Can you imagine the number of variables you’d need to describe crop failures, population booms, and market bubbles? Thousands? Millions? How many variables of information do you get from the price of blueberries? One. Hayek dreams of compressing a complex multidimensional space of possibilities that includes the state of the world and the states of mind of thousands or millions of agents into a single dimension (i.e. price), inevitably losing a great deal of information in the process.

Information theory was originally developed by Claude Shannon at Bell Labs to understand communication. His big insight was that you could understand communication over telephone wires mathematically if you focused not on what was being communicated in specific messages but rather on the complex multidimensional distributions of possible messages. A key requirement for a communication system to work in the presence of noise would be that it could faithfully transmit not just a given message, but rather any message drawn from the distribution. If you randomly generated thousands of messages from the distribution of possible messages, the distribution of generated messages would be an approximation to the actual distribution of messages. If you sent these messages over your noisy communication channel that met the requirement for faithful transmission, it would reproduce an informationally equivalent distribution of messages on the other end.

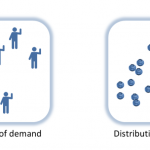
We’ll use Shannon’s insight about matching distributions on either side of a communication channel to match distributions of supply and demand on either side of market transactions. Let’s start with a set of people who want blueberries (demand) and a supply of blueberries. These represent complex multidimensional distributions based on all the factors that go into wanting blueberries (a blueberry superfood fad, advertising, individual preferences) and all the factors that go into having blueberries (weather, productivity of blueberry farms, investment).

In place of Hayek’s aggregation function, information theory lets us re-think the price mechanism’s relationship with information. Stable prices mean a balance of crop failures and crop booms (supply), population declines and population booms (demand), speculation and risk-aversion (demand) — the distribution of demand for blueberries is equal to the distribution of the supply of blueberries. Prices represent information about the differences (or changes) in the distributions. And differences in distributions mean differences in information.

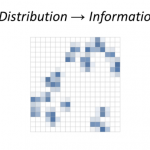
Imagine you have blueberries randomly spread over a table. If you draw a grid over that table, you could imagine deciding to place a blueberry on a square based on the flip of  a coin (a 1 or a 0). That is one bit of information. Maybe for some of the squares, you flip the coin two or more times. That’s two or more bits.

Now say you set up a distribution of buyers on an identical grid using the same process. If you flipped more coins for the buyers than the blueberries on the corresponding squares, that represents a difference in information (and likely an excess demand).

There can be an information difference even if there’s no difference between the results of the coin flips. For example, you can get one blueberry on a square because you flipped a coin once and it came up heads or you flipped a coin twice and it came up heads once and tails once. However as the number of coin flips becomes enormous in a huge market, the difference between the results of the coin flips (excess supply or demand) will approximate the difference in the information in the coin flips. This is an important point about when markets work that we will come back to later. It is also important to note that these are not just distributions in space, but can be distributions in time. The future distribution of blueberries in a functioning market matches the demand for blueberries, and we can consider the demand distribution information flowing from that future allocation of blueberries to the present through transactions.

Coming back to a stable equilibrium means information about the differences in one distribution (i.e. the number of coin flips) must have flowed (through a communication channel) to the other distribution via transactions between buyers and sellers at market prices. We can call one distribution D and the other S for supply and demand. The price is then a function of changes (Δ or “delta”) in D and changes in S:

p = f(ΔD, ΔS)

Price is a function of changes in demand and changes in supply. That’s Economics 101. But what is the function describing the relationship?  We know that an increase in S that’s bigger than an increase in D generally leads to a falling price, while an increase in D that is bigger than the increase in S generally leads to a rising price. If we think in terms of distributions of demand and supply, we can try

p = ΔD/ΔS

for our initial guess. Instead of a aggregating information into a price, which we can’t do without throwing away information, we have a price detecting the flow of information. Constant prices tell us nothing, but price changes tell us information has flowed (or been lost) between one distribution and the other. And we can think of this information flowing in either space or time if we think of the demand distribution as the future allocation of supply.

This picture also gets rid of the dimensionality problem: the distribution of demand can be as complex and multidimensional (i.e. depend on as many variables) as the distribution of supply. The single dimension represented by the price now only measures the single dimension of information flow.

Marginalism and supply and demand

Chris Hayes also mentions marginalism. It’s older than Friedman or Hayek, going back at least to William Jevons. In his 1892 thesis, Irving Fisher tried to argue (crediting Jevons and Alfred Marshall) that if you have gallons of one good A and bushels of another good B that were exchanged for each other, then the last increment (the marginal unit) was exchanged at the same rate as A and B, i.e.

ΔA/ΔB = A/B

calling both sides of the equation the price of B in terms of A. Note that the left side is our price equation above (p = ΔD/ΔS), just in terms of A and B (you could call A the demand for B). In fact, we can get a bit more out of this equation if we say

pₐ = ΔA/ΔB = A/B

We add a little subscript a to remind us that this is the price of B in terms of A. If you hold A constant and increase B (supply), the price goes down. For fixed demand, increasing supply causes prices to fall – a demand curve. Likewise if you hold B constant and increase A, the price goes up – a supply curve. However if we take tiny increments of A and B and use a bit of calculus (ΔA/ΔB becomes dA/dB) the equation becomes a differential equation that can be solved. In fact, it is one of the oldest differential equations to be solved (by Bernoulli in the late 1600s). However, the solution tells us that A is linearly proportional to B. It’s a quite limited model of the supply-demand relationship.

Fisher attempts to break out of this limitation by introducing utility functions in his thesis. However thinking in terms of information can again help us.

If we think of our distribution of A and distribution of B (like the distribution of supply and demand), each “draw” event from those distributions (like a draw of a card, a flip of one or more coins, or roll of a die) contains I₁ information (a flip of a coin contains 1 bit of information) for A and I₂ for B. If the distribution of A and B are in balance (“equilibrium”). Each draw event from each distribution (a transaction event) will match in terms of information. Now it might cost two or three gallons of A for each bushel of B, so the number of draws on either side will be different in general, but as long as the number of draws (n) is large, the total information from those draws will be the same:

n₁ · I₁ = n₂ · I₂

Rearranging, we have

n₁ · (I₁ / I₂) = n₂

We’ll call I₁/I₂ = k (for reasons we’ll get into later) so that

k · n₁ = n₂

Now say the smallest amount of A is ΔA and likewise for B. One bushel or one gallon, say. That means

n₁ = A/ΔA

n₂ = B/ΔB

i.e. the number of gallons of A is the total amount of A divided by 1 gallon of A (i.e. ΔA). Putting this together and rearranging a bit we have

ΔA/ΔB = k · A/B

This is just Fisher’s equation again except there’s our coefficient k in it expressing the information relationship, making the solution to the differential equation mentioned above a bit more interesting than being linearly proportional — now log(A) = k log(B) + b, where b is another constant. The supply and demand relationship found by holding either A or B constant and varying the other is also more complex than the one you obtain from Fisher’s equation (it depends on k). It’s essentially a more generalized marginalism where we no longer assume k = 1. But there’s a more useful bit of understanding you get from this approach that you don’t get from simple price signaling. What we have is information flowing between A and B, and we’ve assumed that information transfer is perfect. But markets aren’t perfect, and all we can really say is that the most information that can get from the distribution of A to the distribution of B is all of the information in the distribution of A. Basically

n₁ · I₁ ≥ n₂ · I₂

Following through with this insight in the derivation above, we find

p = ΔA/ΔB ≤ k · A/B

Because the information flow from A can never be greater than A’s total information, and will mostly be less than that total, the observed prices in a real economy will most likely fall below the ideal market prices. Another way to put it is that ideal markets represent a best-case scenario, one out of a huge space of possible scenarios.

There’s also another assumption in that derivation – that the number of transaction events is large, as we mentioned before. So even if the information transfer was ideal, the traditional price mechanism only applies in markets that have a large volume of trade. That means prices for rare cars or salaries for unique jobs likely do not represent accurate information about the underlying complex multidimensional distributions of market supply and demand. Those prices are in a sense arbitrary. They might represent some kind of data (about power, privilege, or negotiation skills), but not necessarily information about the supply and demand distributions or the market allocation of resources. In those cases, we can’t really know from the price alone.

Another insight we get is that supply and demand doesn’t always work in the simple way described in Marshall’s diagrams. We had to make the assumption that A or B was relatively constant while the other changed. In many real world examples we can’t make that assumption. A salient one today is the (empirically incorrect) claim that immigration lowers wages. A naive application of supply and demand (increased supply of labor lowers the price of labor) ignores the fact that more people means not just more labor, but more people to buy goods and services produced by labor. Thinking in terms of information, it is impossible to say that you’ve increased the number of labor supply events without increasing the number of labor demand events, so you must conclude A and B must both change. More immigration means a larger economy; the effect on prices or wages does not simply follow from supply and demand based on a population increase.

Instead of the simplified picture of ideal markets and forces of supply and demand, we have the picture advocates on the left (and to be fair most  economists) try to convey of not only market failures and inefficiency but more complex interactions of supply and demand. Instead of starting with the best-case scenario, we start with a huge space of possible scenarios — all but one of them less-than-best.

However, it is also possible through collective action to mend or mitigate some of these failures. We shouldn’t assume that just because a market spontaneously formed or produced a result, that it is working optimally, and we shouldn’t assume that because a price went up either demand went up or supply went down. In that case, the market might have just gotten better at detecting information flow that was already happening. We might have gone from non-ideal information transfer where n₁ · I₁ ≥ n₂ · I₂ to something closer to ideal where n₁ · I₁ ≈ n₂ · I₂, meaning the observed price got closer to the higher ideal price.

The equations above were originally derived a bit more rigorously by physicists Peter Fielitz and Guenter Borchardt in a paper published in 2011 titled “A generalized concept of information transfer” (there is also an arXiv preprint). The paper includes both the ideal information transfer (information equilibrium) and non-ideal information transfer scenarios. They call the coefficient k the information transfer index. As they state in their abstract, information theory provides shortcuts that allow one to deal with complex systems. Fielitz and Borchardt primarily had natural complex systems in mind, but as we have just seen, the extension to social complex systems — especially pointing out the assumptions necessary for markets to function — is straightforward.

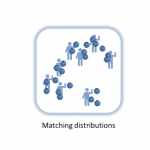
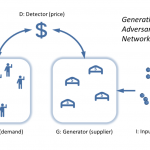
The market as an algorithm

The picture above is of a functioning market as an algorithm matching distributions by raising and lowering a price until it reaches a stable price. In fact, this picture is of a specific machine learning algorithm called Generative Adversarial Networks (GAN, described in this Medium article or in the original paper) that has emerged recently. Of course, the idea of the market as an algorithm to solve a problem is not new. For example one of the best blog posts of all time (in my opinion) talks about linear programming as an algorithm, giving an argument for why planned economies will likely fail, but the same argument implies we cannot check the optimality of the market allocation of resources, therefore claims of markets as optimal are entirely faith-based. The Medium article uses a good analogy using a painting, a forger, and a detective, but I will recast it in terms of the information theory description.

Instead of the complex multidimensional distributions, here we have blueberry buyers and blueberry sellers. The “supply” (B from above) is the generator G, the demand A is the “real data” R (the information the deep learning algorithm is trying to learn). Instead of the random initial input I — coin tosses or dice throws — we have the complex, irrational, entrepreneurial, animal spirits of people. We also have the random effects of weather on blueberry production. The detector D (which is coincidentally the terminology Fieltiz and Borchardt used) is the price p. When the detector can’t tell the difference between the distribution of demand for blueberries and the distribution of the supply of blueberries (i.e. when the price reaches a relatively stable value because the distributions are the same), we’ve reached our solution (a market equilibrium).

Note that the problem the GAN algorithm tackles can be represented by the two-player minimax game from game theory. The thing is that with the wrong settings, algorithms fail and you get garbage. I know this from experience in my regular job researching machine learning, sparse reconstruction, and signal processing algorithms. Therefore depending on the input data (especially data resulting from human behavior), we shouldn’t expect to get good results all of the time. These failures are exactly the failure of information to flow from the real data to the generator through the detector – the failure of information from the demand to reach the supply via the price mechanism.

When asked by Quora what the recent and upcoming breakthroughs in deep learning are, Yann LeCun, director of AI research at Facebook and a professor at NYU, said:

The most important one, in my opinion, is adversarial training (also called GAN for Generative Adversarial Networks). This is an idea that was originally proposed by Ian Goodfellow when he was a student with Yoshua Bengio at the University of Montreal (he since moved to Google Brain and recently to OpenAI).

This, and the variations that are now being proposed is the most interesting idea in the last 10 years in ML, in my opinion.

Research into these deep learning algorithms and information theory may provide insight into economic systems.

An interpretation of economics for the left

So again, Hayek had a fine intuition: prices and information have some relationship. But he didn’t have the conceptual or mathematical tools of information theory to understand the mechanisms of that relationship — tools that emerged with Shannon’s key paper in 1948, and that continue to be elaborated to this day to produce algorithms like generative adversarial networks.

The understanding of prices and supply and demand provided by information theory and machine learning algorithms is better equipped to explain markets than arguments reducing complex distributions of possibilities to a single dimension, and hence, necessarily, requiring assumptions like rational agents and perfect foresight. Ideas that were posited as articles of faith or created through incomplete arguments by Hayek are not even close to the whole story, and leave you with no knowledge of the ways the price mechanism, marginalism, or supply and demand can go wrong. Those arguments assume and (hence) conclude market optimality. Leaving out the failure modes effectively declares many social concerns of the left moot by fiat. The potential and actual failures of markets are a major concern of the left, and are frequently part of discussions of inequality and social justice.

The left doesn’t need to follow Chris Hayes’ advice and engage with Hayek, Friedman, and neoclassical economics. The left instead needs to engage with a real world vision of economics that recognizes the limited scope of ideal markets and begins with imperfection as the more useful default scenario. Understanding economics in terms of information flow is one way of doing that.

2017 May 18